Nonlinear Buckling Analysis Setup in Simcenter Nastran
Blog Article | February 13, 2026
Author: Andy Haines | Principal Application Engineer
- Over 30 years of Femap experience
- Over 25 years as a member of the Simcenter Femap Development team, involved in almost all aspects of planning, developing, selling, marketing, and supporting the Femap product
- Taught over 50 Femap training classes to engineers of all experience levels
Introduction
Nonlinear buckling analysis offers a more realistic evaluation of structural stability than linear eigenvalue methods, particularly for thin or flexible structures under compression. This article explains what nonlinear buckling is, when it should be used, and how a practical nonlinear buckling workflow is typically set up in Simcenter Nastran. The emphasis is on clear modeling steps, solver behavior, and realistic expectations—without overcomplicating the process. This blog zones into the fundamentals of nonlinear buckling and outlines a step-by-step approach for setting up such analyses in Simcenter Nastran, with attention to practical modeling decisions.
Buckling is a common and often governing failure mode for structures subjected to compressive loading. Panels, shells, stiffened plates, and slender members may lose stability well before material strength limits are reached. Linear buckling analysis is frequently used during early design, but its simplifying assumptions can lead to overly optimistic predictions.
Nonlinear buckling analysis addresses these limitations by allowing stiffness to evolve as the structure deforms under load. This makes it especially relevant for safety-critical industries, including aerospace, automotive structures, civil engineering, and energy systems where thin-walled structures and high utilization levels are common.
What Is Nonlinear Buckling?
Nonlinear buckling analysis evaluates structural stability while accounting for nonlinear effects that influence stiffness and equilibrium as loads are applied incrementally. Unlike linear eigenvalue buckling—which assumes a perfect geometry and linear elastic behavior—nonlinear buckling follows the actual load–deformation response of the structure.
Key Characteristics Include:
- Incremental or stepped load application
- Stiffness updating as deformation develops
- Explicit tracking of equilibrium as instability is approached
- Ability to study behavior near and beyond the buckling point
Instead of producing a single buckling factor, nonlinear analysis provides insight into how and when a structure loses stability.
Why Nonlinear Buckling Analysis Is Important
Linear buckling analysis predicts an idealized critical load based on the initial stiffness matrix. While useful for identifying likely buckling modes, it does not represent how real structures behave under increasing load.
Nonlinear Buckling Analysis Is Important Because It:
- Captures stiffness degradation due to large deformations
- Produces more realistic estimates of critical load levels
- Supports decision-making for safety-critical designs
- Provides context for whether post-buckling strength may exist
For modern lightweight designs, nonlinear buckling is often required to move from theoretical capacity to realistic structural assessment.
Linear vs. Nonlinear Buckling
Linear Buckling Analysis:
- Assumes small displacements and linear elastic response
- Solves an eigenvalue problem based on the undeformed structure
- Predicts idealized buckling loads and shapes
- Fast and effective for early design screening
Nonlinear Buckling Analysis:
- Includes geometric nonlinearity and, if needed, material nonlinearity
- Applies loads incrementally with stiffness updates
- Follows the equilibrium path toward instability
- More computationally demanding and sensitive to setup
In practice, linear buckling is best used to guide and inform nonlinear studies rather than replace them.
When to Use Nonlinear Buckling Analysis
Nonlinear Buckling Analysis Is Most Appropriate For:
- Thin-walled or flexible structures under compressive or combined loading
- Cases involving large deflections, where stiffness changes significantly before buckling
- Applications where linear buckling margins are insufficient for design confidence
- Safety-critical industries, including aerospace, automotive structures, civil engineering, and energy systems
When buckling capacity directly affects certification, margins of safety, or allowable loads, nonlinear analysis becomes essential.
Key Concepts in Nonlinear Buckling
Geometric Nonlinearity
Large displacements and rotations modify the stiffness of a structure as it deforms. Enabling geometric nonlinearity is fundamental for capturing buckling behavior.
Material Nonlinearity
Plasticity or other nonlinear material behavior may influence buckling or collapse. Many analyses begin with linear elastic materials and add plasticity only when post-buckling or failure behavior is of interest.
Equilibrium Path and Post-buckling Realm
Nonlinear analysis traces the equilibrium path of the structure as load increases. Buckling corresponds to a loss of stiffness or change in this path, while post-buckling describes the response beyond the initial instability.
Arc-Length / Riks vs. Newton-Raphson Solvers
Standard Newton-Raphson solvers often struggle near instability points. Arc-length or modified Riks methods are designed to follow equilibrium paths through limit points and are commonly used in nonlinear buckling problems.
Simcenter Nastran Nonlinear Buckling Setup
Step 1
Apply Material Properties
Begin with linear elastic material behavior for baseline studies. Introduce plasticity or other nonlinear effects only when the analysis objectives require it.
Step 2
Define Geometry and Mesh
Use element types appropriate for buckling behavior—typically shell elements for thin-walled structures or solid elements where thickness effects matter. Mesh density should be sufficient to capture expected buckling modes without excessive distortion.
Step 3
Define Boundary Conditions
Boundary conditions strongly influence buckling response. Carefully model supports, symmetry, and constrained degrees of freedom to reflect the physical system without artificially stiffening the structure.
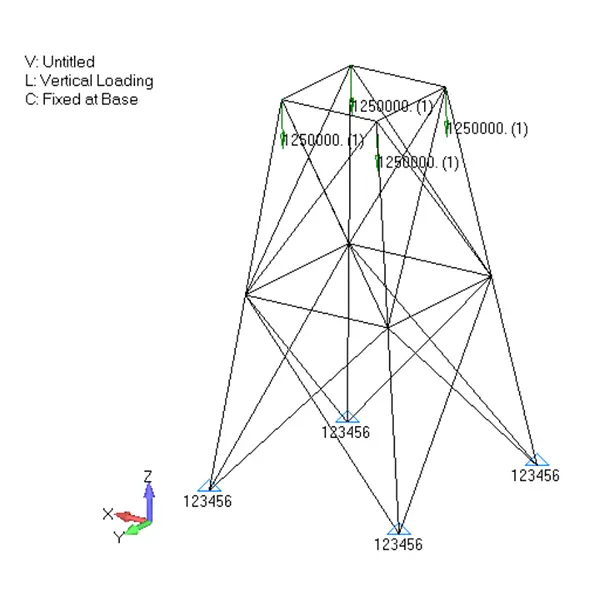
Step 4
Apply Loads
Apply compressive, pressure, or combined loads in a realistic manner. Loads are typically ramped incrementally so the solver can track stiffness changes as deformation develops.
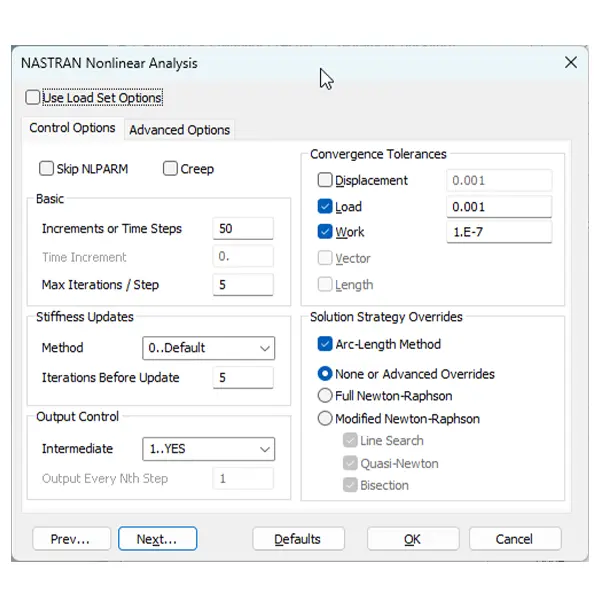
Step 5
Run Nonlinear Static or Linear Buckling Analysis (Pre-Buckling) - OPTIONAL
Perform a nonlinear static analysis with geometric nonlinearity enabled to establish the stressed configuration prior to instability or perform a linear buckling analysis for comparison.
Step 6
Perform Prestress Normal Modes / Eigenvalue Extraction
Extract buckling modes using the stiffness matrix from the nonlinear static solution. These modes help estimate critical load levels and identify likely instability shapes.
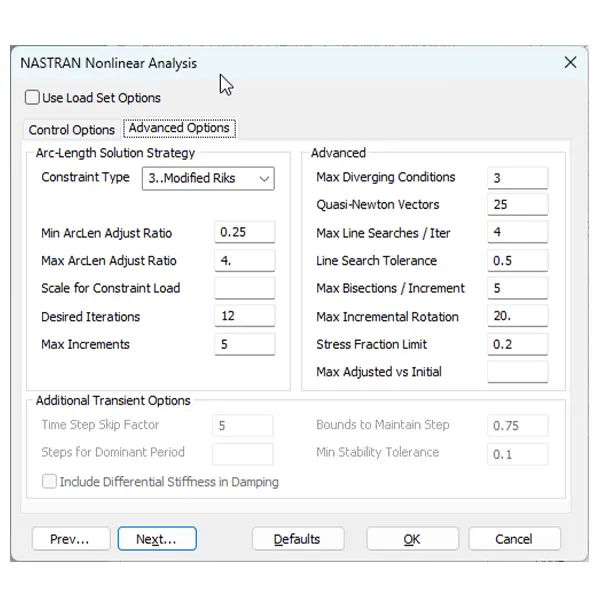
Step 7
Use Arc-Length or Modified Riks Method
When tracing instability directly, arc-length or modified Riks methods allow the solution to continue through limit points and capture unstable response regions.
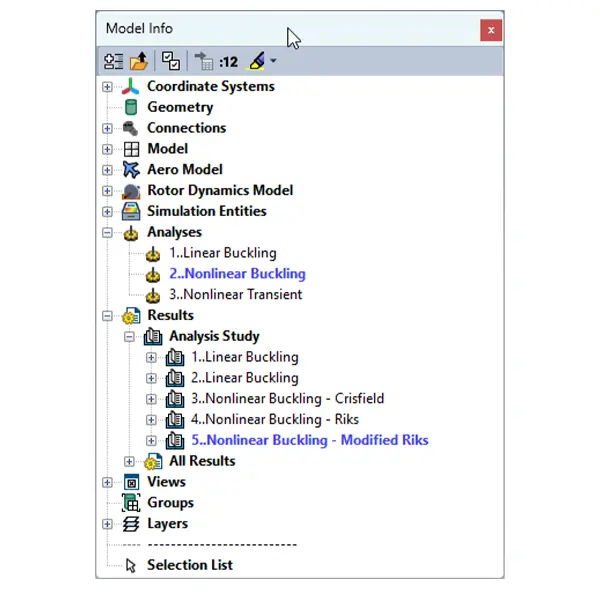
Step 8
Save Outcomes
Track displacements, stresses, load factors, and convergence behavior to fully understand how the structure responds as buckling is approached.
Convergence & Other Considerations
Nonlinear buckling analyses are inherently sensitive and may require adjustment to achieve stable solution.
Common Practices Include:
- Refining load step sizes near expected instability
- Monitoring convergence norms and equilibrium residuals
- Adjusting solver controls for problems involving snap-through or stiffness loss
Experience plays a major role here; as familiarity increases, setup effort and solution time typically decrease. In some cases, a perfectly symmetric model and loading condition may not naturally exhibit buckling behavior. Small, intentional perturbations are therefore sometimes introduced to break symmetry and allow the solver to follow a realistic instability path. These disturbances are typically very small relative to the structure’s overall dimensions and are intended to influence how buckling initiates rather than significantly altering the predicted load level.
As with solver controls and load stepping, the use and magnitude of such perturbations often require iteration. Experience with similar structures and loading conditions helps engineers apply them judiciously without compromising result fidelity.
Post-Buckling Analysis
Nonlinear buckling analysis generally identifies the onset of instability, not ultimate collapse. Some structures retain load-carrying capacity after buckling, while others do not.
To Study Post-Buckling Behavior:
- Nonlinear static analysis may be sufficient for mild post-buckling
- Nonlinear transient or implicit dynamic analysis can handle severe instability or snap-through
- Inertia effects help the solver pass unstable equilibrium points
This is particularly relevant for aircraft panels, cylindrical shells, and reinforced plates where post-buckling strength contributes to allowable design loads.
Advantages & Limitations of Nonlinear Buckling in Simcenter Nastran
Advantages
- More realistic representation of structural response
- Captures stiffness changes prior to instability
- Enables assessment beyond idealized buckling loads
Limitations
- More complex setup than linear buckling
- Potential convergence difficulties near instability
- Increased computational cost
Best Practices
- Use linear buckling to inform nonlinear setup
- Refine mesh and load stepping near critical regions
- Review convergence behavior carefully at each stage
Conclusion & Key Takeaways
Nonlinear buckling analysis is a critical tool for accurately assessing the stability of thin, lightweight, and highly loaded structures. By allowing stiffness to evolve with deformation, nonlinear methods provide insight that linear buckling alone cannot deliver.
With a structured workflow and realistic expectations, nonlinear buckling analysis in Simcenter Nastran becomes a practical and valuable part of an engineer’s simulation toolkit—supporting safer designs and better-informed decisions.
Key Takeaways
- Linear buckling provides idealized estimates and mode shapes
- Nonlinear buckling captures stiffness evolution under load
- Arc-length methods improve robustness near instability
- Post-buckling behavior often requires advanced nonlinear analysis
- Experience significantly improves efficiency and reliability
